最近把周志华的《机器学习》西瓜书系统的复习一遍,整理一些笔记。主要介绍下神经网络的基本单元-神经元;其次介绍下常用的激活函数;经典BP算法的推导和深度学习的简述。
神经元简述
神经网络中最基本的单元是一直沿用至今的“M-P神经元”,神经元接收到来自 n 个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过“激活函数”输出(图中 $f$ 即为激活函数)。
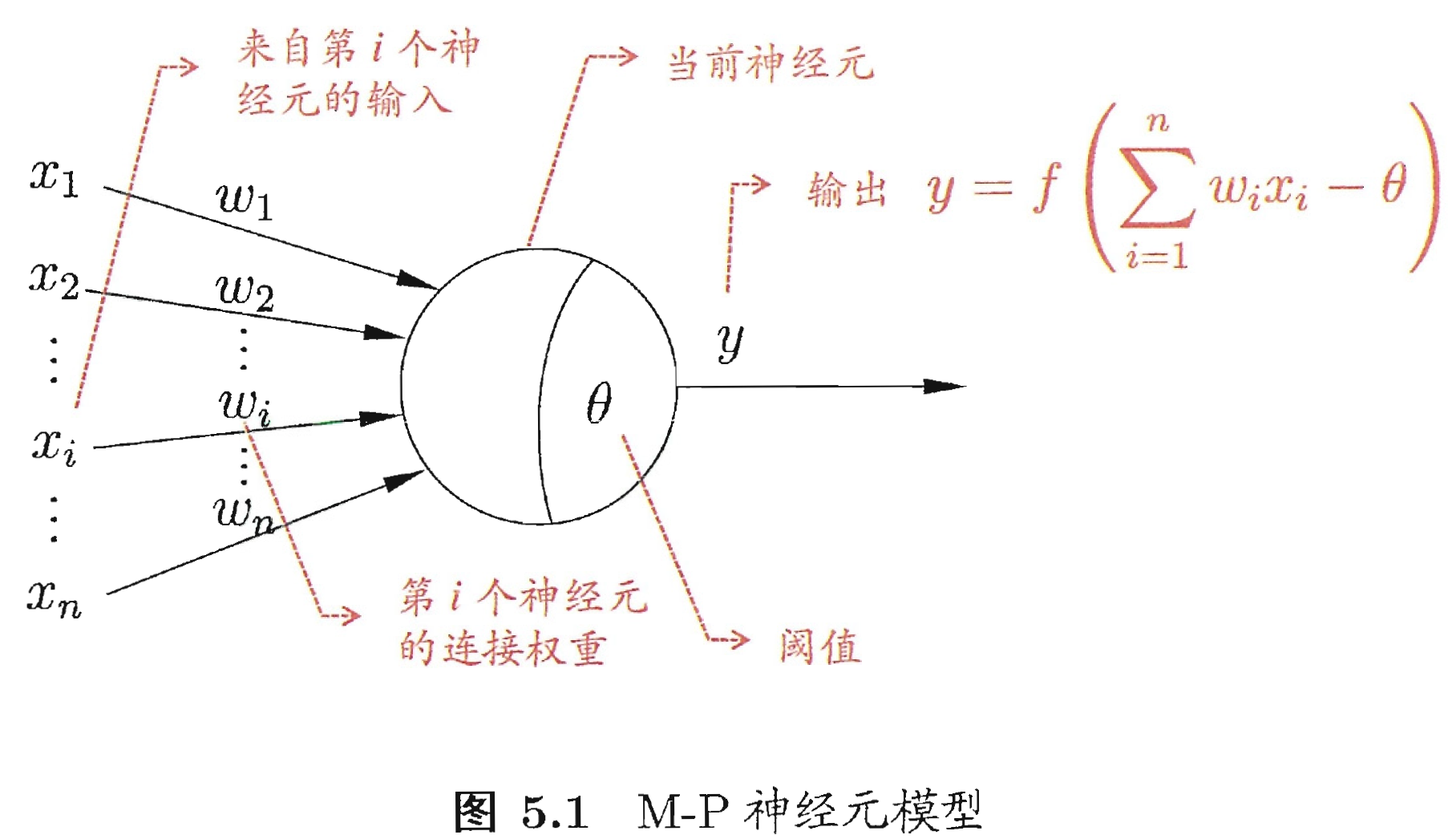
感知机是两层神经元组成,即输入层和输出层。它是最简单的神经网络,学习得是一个超平面,但其表达能力非常有限,例如“异或”问题它就表达学习不了。要解决这类问题,所以需要考虑多层功能的神经元。即利用感知机神经元构成多层神经网络。
常用激活函数
激活函数是上述神经元中的 $f$ 函数,这里介绍下常用的激活函数。
阶跃函数:即
$f(x) = \left\{\begin{matrix} 1, & x \geqslant 0 & \\ 0, & x < 0 & \end{matrix}\right.$,优点:形式简单;缺点:梯度为0,不能用于反向传播过程。因为不可导,该激活函数不常用。sigmoid函数:即
$f(x) = \frac{1}{1 + e^{-x}} $, 它是一个logistic函数,优点:连续可微;缺点:函数在原点周围不对称,得到的值都是正的;梯度变化在[-3,3]外渐趋平坦。tanh函数:与sigmoid函数非常相似,即
$tanh(x) = 2 \cdot sigmoid(2x) - 1$,x轴方向把sigmoid压缩;y轴方向扩大1倍同时下移1个单位。优点:连续可导且关于原点对称;缺点:梯度变化在非[-3,3]区间内渐趋平坦(与sigmoid类似)。ReLU函数:即
$f(x) = \left\{\begin{matrix} x, & x \geqslant 0 & \\ 0, & x < 0 & \end{matrix}\right.$,其中间断点$x=0$处导数指定为0。 优点:不会同时激活所有的神经元,若输入值是负的,ReLU函数会转换为0,而神经元不被激活,意味着一段时间只有少量的神经元被激活,这种稀疏性使其变得高效且易于计算;缺点:当小于0时,梯度为0,权重不会更新,会产生死神经元。Leaky ReLU函数:即
$ f(x) = \left\{\begin{matrix} x, & x \geqslant 0 & \\ ax, & x < 0 & \end{matrix}\right.$,其中间断点$x=0$处导数指定为0。 是ReLU函数的变体(另外还有PReLU等变体),这里的$a$是一个很小的值(在PReLU是可以学习参数$a$的),如 0.01。优点:除ReLU的优点外,同时解决了ReLU产生死神经元的问题。softmax函数:即
$f(x) = \frac{e^{z_j}}{\sum_{k=1}{K}e^{z_k}}$在处理多分类问题时,softmax函数将压缩每个类在0到1之间,并除以输出总和。比如,我们输入 [1.2, 0.9, 0.75] ,当应用softmax函数时,得到 [0.42, 0.31, 0.27] 。softmax函数最好在分类器的输出层使用。
神经网络激活函数的选择:根据问题的性质,主要以神经网络更快更方便地收敛作出更好的选择。用于分类器时,sigmoid函数及其组合通常效果更好;由于梯度消失的问题,有时要避免使用sigmoid和tanh函数,ReLU函数是一个通用的激活函数,目前在大多数情况下使用;如果神经网络中出现死神经元,那PReLU函数是最好的选择,ReLU函数只能在隐层中使用。
可以先从ReLU函数开始,如果ReLU函数没有提供最优结果,再常试其他激活函数。
误差反向传播推导
训练多层网络,误差逆传播(error BackPropagation,简称BP)算法是最经典的算法。下面手推下BP。
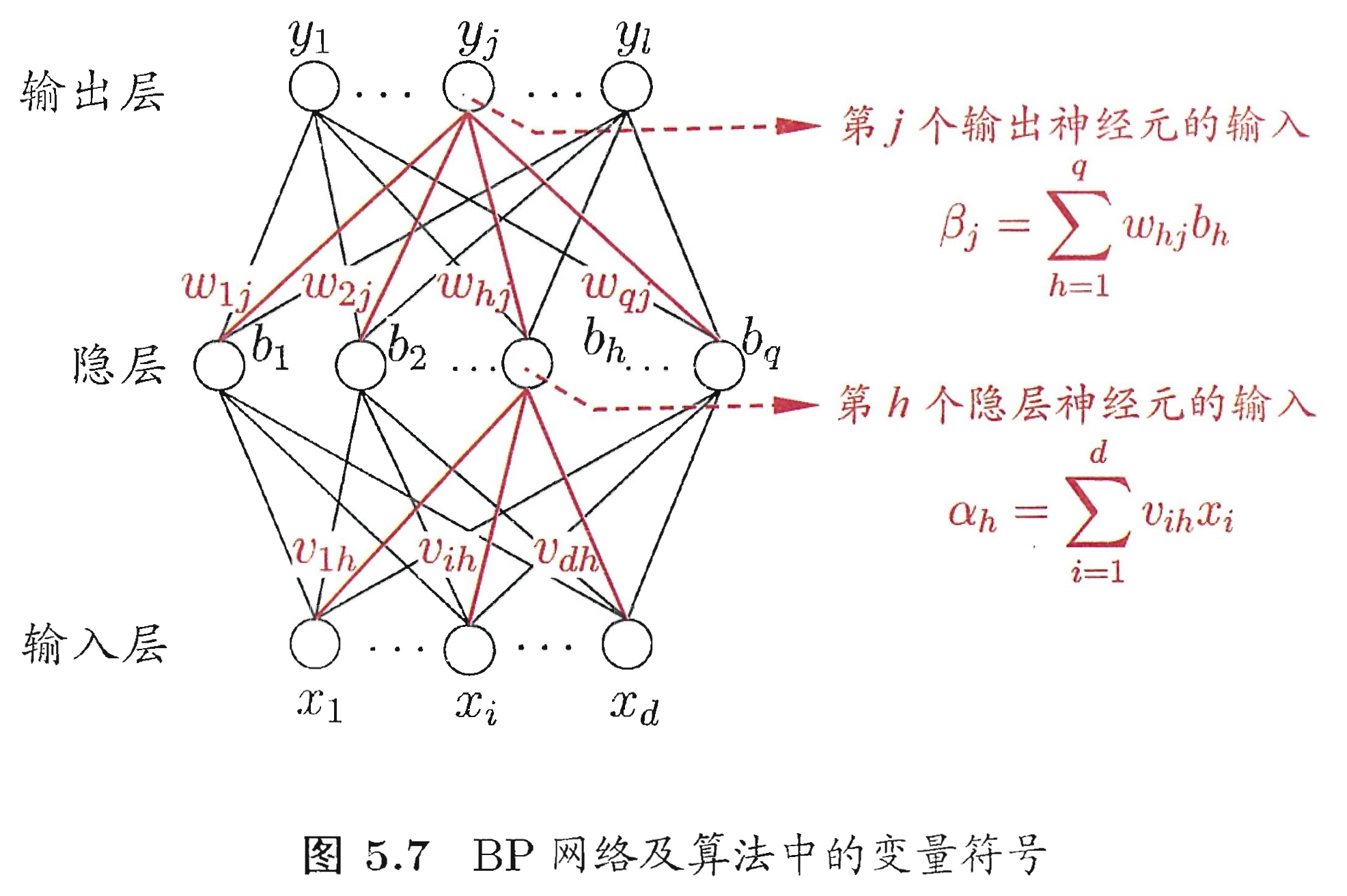
训练集 $(x_k, y_k)$ ,神经网络的输出为 $\hat{y}_k = (\hat{y}_1^k, \hat{y}_2^k, ..., \hat{y}_l^k)$ ,即 $ \hat{y}_j^k = f(\beta_j - \theta_j)$ ,
在 $(x_k, y_k)$ 上的均方误差为 $E_k = \frac{1}{2} \sum_{j=1}^{l} ( \hat{y}_j^k - y_j^k )^2$ 。
上图中有 $(d \times q \ + q \times l \ + q \ + \ l)$ 个 参数需要学习。输入层到隐层有 $d \times q$ 个权值、隐层到输出层有 $q \times l$ 个权值、$q$ 个隐层阈值、$l$ 个输出层阈值。
BP算法基于梯度下降策略,以目标的负梯度方向对参数进行调整,对式 $E_k$ 的误差,给定学习率 $\eta$ ,有 $\Delta w_{hj} = - \eta \frac{\partial E_k}{\partial w_{hj}}$ 。
其中 $\frac{\partial E_k}{\partial w_{hj}}$ 是利用链式求导法则,即 $\frac{\partial E_k}{\partial w_{hj}} = \frac{\partial E_k}{\partial \hat{y}_j^k} \cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial w_{hj}}$ ;
其中 $\frac{\partial E_k}{\partial \hat{y}_j^k} \cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j} = (\hat{y}_j^k - y_j^k) \cdot (1 - \hat{y}_j^k) \cdot \hat{y}_j^k$ ,令 $g_j = - \frac{\partial E_k}{\partial \hat{y}_j^k} \cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j} = - (\hat{y}_j^k - y_j^k) \cdot (1 - \hat{y}_j^k) \cdot \hat{y}_j^k$ ;而 $\frac{\partial \beta_j}{\partial w_{hj}} = b_h$ ;
所以 $\Delta w_{hj} = - \eta \frac{\partial E_k}{\partial w_{hj}} = \eta \cdot g_j \cdot b_h$ ,同理 $\theta_j = - \eta \cdot g_j$ 。
对于 $v_{ih}$ 和 $\theta_h$ 的更新,同样是利用链式法则求导,即 $\frac{\partial E_k}{\partial v_{ih}} = \frac{\partial E_k}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial b_h} \cdot \frac{\partial b_h}{\partial \alpha_h} \cdot \frac{\partial \alpha_h}{\partial x_i}$ ;
其中 $\frac{\partial E_k}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial b_h} = \sum_{j=1}^l g_j \cdot w_{hj}$ ,$\frac{\partial b_h}{\partial \alpha_h} = (1-b_h) \cdot b_h$ ,$\frac{\partial \alpha_h}{\partial x_i} = x_i$ ;令 $e_h = - \frac{\partial E_k}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial b_h} \cdot \frac{\partial b_h}{\partial \alpha_h}$ ;
所以 $\Delta v_{ih} = \eta \cdot e_h \cdot x_i$ ,同理 $\Delta \gamma_h = - \eta \cdot e_h$ 。
上述推导是标准BP算法,我们的最终目标是要最小化训练集 $D$ 上的累积误差,即 $E = \frac{1}{m} \cdot \sum_{k=1}^{m} E_k$ ,如果类似推导出基于累积误差最小化的更新规则,就得到了累积误差逆传播算法。累积BP算法与标准BP算法都很常用。在很多任务中,累积误差下降到一定程度后,进一步下降会用标准BP算法。
深度学习
典型深度学习模型就是很深层的神经网络,通过增加隐层层数来提高神经网络的表征能力。提高表征能力的方法有 (1)增加层数;(2)增加神经元;从增加模型复杂度来看,增加层数显得比增加神经元更有效。因为增加隐层数不仅增加了拥有激活函数的神经元数目,还增加了激活函数嵌套的层数。
在深度学习中,经典的BP算法训练,误差在多隐层内逆传播时,往往会“发散”而不能收敛到稳定状态。无监督逐层训练是多隐层网络训练的有效手段。基本思想:每次训练一层隐层,训练时将上一层隐结点的输出作为输入,而本层隐层的输出作为下一层隐层的输入,这称为“预训练”(pre-training);在预训练全部完成后,再对整个网络进行“微调”(fine-tuning)训练。 “预训练+微调”的做法可视为将大量参数分组,对每组先找到局部解,然后再基于这些局部较优解寻找全局最优解。
另一种节省训练开销的策略是“权共享”,即让一组神经元使用相同的连接权。这个策略在卷积神经网络(CNN)中有体现。
另一个角度理解深度学习,深度学习是逐层加工,逐层将初始的“低层”特征表示转化为“高层”特征,可以看作是在做特征工程。当特征学得差不多的时候,最后套一个输出层即可进行分类。
总结
笔记主要总结学习了下神经网络。主要是神经元、常用的激活函数、经典BP反向传播算法的推导和深度学习。深度学习发展非常快,近几年在推荐系统领域广泛应用,后期有时间学习下深度学习在推荐系统里的应用。 激活函数的使用技巧要在实践中才能体会到,后续尝试下跑一些深度学习的demo。
参考文献
《机器学习》西瓜书,周志华